Global-warming potential
Global-warming potential (GWP) is a relative measure of how much heat a greenhouse gas traps in the atmosphere. It compares the amount of heat trapped by a certain mass of the gas in question to the amount of heat trapped by a similar mass of carbon dioxide. A GWP is calculated over a specific time interval, commonly 20, 100 or 500 years. GWP is expressed as a factor of carbon dioxide (whose GWP is standardized to 1). For example, the 20 year GWP of methane is 72, which means that if the same mass of methane and carbon dioxide were introduced into the atmosphere, that methane will trap 72 times more heat than the carbon dioxide over the next 20 years.[1]
The substances subject to restrictions under the Kyoto protocol either are rapidly increasing their concentrations in Earth's atmosphere or have a large GWP.
The GWP depends on the following factors:
- the absorption of infrared radiation by a given species
- the spectral location of its absorbing wavelengths
- the atmospheric lifetime of the species
Thus, a high GWP correlates with a large infrared absorption and a long atmospheric lifetime. The dependence of GWP on the wavelength of absorption is more complicated. Even if a gas absorbs radiation efficiently at a certain wavelength, this may not affect its GWP much if the atmosphere already absorbs most radiation at that wavelength. A gas has the most effect if it absorbs in a "window" of wavelengths where the atmosphere is fairly transparent. The dependence of GWP as a function of wavelength has been found empirically and published as a graph.[2]
Because the GWP of a greenhouse gas depends directly on its infrared spectrum, the use of infrared spectroscopy to study greenhouse gases is centrally important in the effort to understand the impact of human activities on global climate change.
Contents |
Calculating the global-warming potential
Just as radiative forcing provides a simplified means of comparing the various factors that are believed to influence the climate system to one another, global-warming potentials (GWPs) are one type of simplified index based upon radiative properties that can be used to estimate the potential future impacts of emissions of different gases upon the climate system in a relative sense. GWP is based on a number of factors, including the radiative efficiency (infrared-absorbing ability) of each gas relative to that of carbon dioxide, as well as the decay rate of each gas (the amount removed from the atmosphere over a given number of years) relative to that of carbon dioxide.[3]
The radiative forcing capacity (RF) is the amount of energy per unit area, per unit time, absorbed by the greenhouse gas, that would otherwise be lost to space. It can be expressed by the formula:
where the subscript i represents an interval of 10 inverse centimeters. Absi represents the integrated infrared absorbance of the sample in that interval, and Fi represents the RF for that interval.
The Intergovernmental Panel on Climate Change (IPCC) provides the generally accepted values for GWP, which changed slightly between 1996 and 2001. An exact definition of how GWP is calculated is to be found in the IPCC's 2001 Third Assessment Report. The GWP is defined as the ratio of the time-integrated radiative forcing from the instantaneous release of 1 kg of a trace substance relative to that of 1 kg of a reference gas:
where TH is the time horizon over which the calculation is considered; ax is the radiative efficiency due to a unit increase in atmospheric abundance of the substance (i.e., Wm−2 kg−1) and [x(t)] is the time-dependent decay in abundance of the substance following an instantaneous release of it at time t=0. The denominator contains the corresponding quantities for the reference gas (i.e. CO2). The radiative efficiencies ax and ar are not necessarily constant over time. While the absorption of infrared radiation by many greenhouse gases varies linearly with their abundance, a few important ones display non-linear behaviour for current and likely future abundances (e.g., CO2, CH4, and N2O). For those gases, the relative radiative forcing will depend upon abundance and hence upon the future scenario adopted.
Since all GWP calculations are a comparison to CO2 which is non-linear, all GWP values are affected. Assuming otherwise as is done above will lead to lower GWPs for other gases than a more detailed approach would.
Use in Kyoto Protocol
Under the Kyoto Protocol, the Conference of the Parties decided (decision 2/CP.3) that the values of GWP calculated for the IPCC Second Assessment Report are to be used for converting the various greenhouse gas emissions into comparable CO2 equivalents when computing overall sources and sinks.[4]
Importance of time horizon
Note that a substance's GWP depends on the timespan over which the potential is calculated. A gas which is quickly removed from the atmosphere may initially have a large effect but for longer time periods as it has been removed becomes less important. Thus methane has a potential of 25 over 100 years but 72 over 20 years; conversely sulfur hexafluoride has a GWP of 22,800 over 100 years but 16,300 over 20 years (IPCC TAR). The GWP value depends on how the gas concentration decays over time in the atmosphere. This is often not precisely known and hence the values should not be considered exact. For this reason when quoting a GWP it is important to give a reference to the calculation.
The GWP for a mixture of gases can not be determined from the GWP of the constituent gases by any form of simple linear addition.
Commonly, a time horizon of 100 years is used by regulators (e.g., the California Air Resources Board).
Values
Carbon dioxide has a GWP of exactly 1 (since it is the baseline unit to which all other greenhouse gases are compared).
| GWP values and lifetimes from 2007 IPCC AR4 p212 [1] (2001 IPCC TAR [2] in parentheses) |
Lifetime (years) | GWP time horizon | ||
|---|---|---|---|---|
|
|
|
|
||
| Methane | 12 (12) | 72 (62) | 25 (23) | 7.6 (7) |
| Nitrous oxide | 114 (114) | 289 (275) | 298 (296) | 153 (156) |
| HFC-23 (hydrofluorocarbon) | 270 (260) | 12,000 (9400) | 14,800 (12,000) | 12,200 (10,000) |
| HFC-134a (hydrofluorocarbon) | 14 (13.8) | 3,830 (3,300) | 1,430 (1,300) | 435 (400) |
| sulfur hexafluoride | 3200 (3,200) | 16,300 (15,100) | 22,800 (22,200) | 32,600 (32,400) |
Although water vapour has a significant influence with regard to absorbing infrared radiation (which is the green house effect; see greenhouse gas), its GWP is not calculated. Its concentration in the atmosphere mainly depends on air temperature. There is no possibility to directly influence atmospheric water vapour concentration.
See also
- Carbon dioxide equivalent
- Emission factor
- Emission standard
- Radiative forcing
- Total equivalent warming impact
References
- ^ "Global Warming Potentials". Climate Change 1995, The Science of Climate Change: Summary for Policymakers. Technical Summary of the Working Group I Report, page 22.. 1995. http://unfccc.int/ghg_data/items/3825.php. Retrieved 2011-04-26.
- ^ Matthew Elrod, "Greenhouse Warming Potential Model." Based on Journal of Chemical Education, Vol 76, pp. 1702–1705, December 1999
- ^ "Glossary: Global warming potential (GWP)". U.S. Energy Information Administration. http://www.eia.gov/tools/glossary/index.cfm?id=G. Retrieved 2011-04-26. "An index used to compare the relative radiative forcing of different gases without directly calculating the changes in atmospheric concentrations. GWPs are calculated as the ratio of the radiative forcing that would result from the emission of one kilogram of a greenhouse gas to that from the emission of one kilogram of carbon dioxide over a fixed period of time, such as 100 years."
- ^ Conference of the Parties (25 March 1998). "Methodological issues related to the Kyoto Protocol". Report of the Conference of the Parties on its third session, held at Kyoto from 1 to 11 December 1997 Addendum Part Two: Action taken by the Conference of the Parties at its third session. UNFCCC. http://unfccc.int/resource/docs/cop3/07a01.pdf. Retrieved 17 January 2011.
External links
- 2007 IPCC Fourth Assessment Report (AR4) by Working Group 1 (WG1) and Chapter 2 of that report (Changes in Atmospheric Constituents and in Radiative Forcing) which contains GWP information.
- 2001 IPCC Third Assessment Report (TAR) page on Global-Warming Potentials and Direct GWP.
- List of Global Warming Potentials and Atmospheric Lifetimes from the U.S. EPA
- An overview of the role of H2O as a greenhouse gas from RealClimate
- GWP and the different meanings of CO2e explained
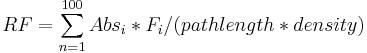
![GWP \left(x\right) = \frac{\int_0^{TH} a_x \cdot \left[x(t)\right] dt} {\int_0^{TH} a_r \cdot \left[r(t)\right] dt}](/2012-wikipedia_en_all_nopic_01_2012/I/ace17b55ef66fded15326b7d25827aa3.png)